✏️ Second Example MM Problem with Expected Value

If you are given probabilities, you will typically need to calculate expected value. (If you see the phrase, “equally likely” you were just given probabilities and will typically need to calculate expected value.)

Typically, we will take an expected value and discount it to the present.

Let’s do a simple example:

✏️ [Value of an unlevered firm]
Suppose you have founded a firm and made a $500,000 investment to purchase and develop the initial assets of that firm. It is a very speculative investment. In one year, it will either be worth $4 million dollars if it pans out or $200,000 if it doesn’t. You estimate the probabilities as follows:

	Value of Assets
20%	$4M
80%	$200K

What is the expected value of the future value of these assets?

Suppose that you want to get out of this business today. You feel that someone else may be able to take it the next stage, so you want to sell. How much can you sell the unlevered firm for? Assume investors are discounting these future cash flows at r=40% given the extreme riskiness involved.

What is the profit from making the original $500K investment and then selling the firm? Should you make the original $500K investment?

✔ Click here to view answer

EV of future value of assets = 20%*4 + 80%*.2 = 0.96
In the future, you “expect” the assets to be worth $960,000.

V_U = E(Value of Assets)/(1+r) = $960,000/(1+40%) = $685,714.29
E() stands for expected value, so E(Value of Assets) stands for “The expected value of Assets in a year.”

The profit from making the investment is:
Costs: $500K
Revenues: $685,714.29
Profit from making the investment and selling the unlevered equity: $685,714.29 - $500,000=$185,714.29 NPV of making the investment and owning the firm yourself = PDV of EV - $500K = $960K/(1+40%)^1 - $500K = $185,714.29 In general, in perfect capital markets, if you make the original investment and then sell the stock, you get the same profit as the NPV if you had just held the company yourself.

🙋‍♂️ Wait a second. So far in this course, we have evaluated projects using NPV. Are we evaluating projects using Expected Value now? Is this a major pivot?
✔ It is an extension/a minor pivot to allow for situations when you don’t know what the future cash flows are and can only calculate an expected value. You calculate the EV and then use NPV and IRR exactly as we have been doing.

🙋‍♂️I calculate an IRR of 92%.
✔If so, you should take the project because 92%>40%. In other words, the IRR rule agrees with the NPV rule.

✏️ Suppose that the risk free rate is 2%. You are considering borrowing $100,000 to make the initial investment of the $500,000. In other words, you will use $100,000 of borrowed money and $400,000 of your own capital to make the $500,000 initial investment.

Compare: “You will partially fund your initial investment of $500,000 using leverage. You will have to repay $100,000 in one year. Your yield is the risk free rate.” The value of the debt today is 100,000/(1+2%) = 98,039.21 . Therefore, the value of the levered equity will be $685,714.29 - $98,039.21 = $587,675.08 =V_L
Compare: “You will partially fund your initial investment of $500,000 using leverage. You issue a zero coupon bond with a face value of $100,000. It is due in 5 years. Your yield is the risk free rate.” The value of the debt today is 100,000/(1+2%)^5 = 90,573.081 . Therefore, the value of the levered equity will be $685,714.29 - 90,573.08 = $595,141.21 =V_L

Side note: let’s assume that EVERYONE agrees on the aforementioned probabilities regarding the value of the assets. Therefore, let’s assume that you can borrow at the risk-free rate.

What will the return to equity-holders be in 1 year?
What is the expected value of the equity in 1 year?

✔ Click here to view answer

First, we calculate out the return to debt-holders in 1 year. In one year, debtholders will be owed $102,000. The assets of the firm will be worth at least $200,000, and we assume that the legal system is efficient enough that they believe that they can get back everything they are owed. (ie they can sue the firm and get back $102,000).

In one year, the value to equity holders will be either

	Value of Assets	Value to Equity (residual claimants)
20%	$4M	4000K-102K=$3,898,000
80%	$200K	$200,000-$102,000=$98,000

🙋‍♀️That is in 1 year not present value

✔Yes!

What is the expected value of the value of the levered equity in 1 year?

EV = 20%$3,898K + 80%$98K = 858%

✏️ Based on MM, what is the value of equity right now.

✔ Click here to view answer

HERE IS HOW NOT TO DO IT. (DON’T DO IT THIS WAY)

“Hey, let’s do what we did before. We’ll just take the expected value and then the present value.
(The expected value of levered equity in one year is 20%*$3,898,000 + 80%*$98,000=$858,000)
DON’T DO THIS BECAUSE YOU DON’T KNOW THE PROPER DISCOUNT RATE. WHEN YOU LEVER UP, THE DISCOUNT RATE CHANGES.
THE FOLLOWING CALCULATION IS NOT VALID BECAUSE THE DISCOUNT RATE ISN’T 40% ANY MORE.
~~V_E = $858,000/(1+40%)=$612,857.14~~ Instead, we will use MM to find a new discount rate for the levered equity.

Instead, use MM #1. V_L= E + D = V_U

V_L = V_U
V_U = $685,714.29 ← this is the value today. We got it by discounting back the EV: $960,000/(1+40%) = $685,714.29

V_L = $685,714.29 = V_E + V_D = V_E + $100,000 (today)
Therefore, the value of the Equity is $685,714.29- $100,000===$585,714.29== (today)

Let’s step back and reflect… Why did we get two different numbers? ~~$612,857.1~~4 (wrong) and $585,714.29 (right). The error in the first manner was that we assumed that the market would discount a levered firm at the same rate as an unlevered firm. But leverage makes things risky, so investors will demand a higher return. IE they won’t be willing to pay $612K. They will only be willing to pay $585K.

✏️ What is the return to equity investors in the levered firm and in the unlevered firm? Are the returns different? If so, why?

✔ Click here to view answer

First let’s calculate the return to the equity investors in the levered firm:
In 1 year, the equity will be worth the following after paying debts

20%*$3,898,000 + 80%*$98,000=$858,000
Right now, it is worth $585,714.29 according to MM. Therefore,
rE = (new-old)/old = new/old - 1 = ($858,000/$585,714.29)-1=46.49%

The levered equity investors are now making 46.49%.

The unlevered equity investors are now making…
In 1 year, the equity will be worth: 20%*4 + 80%*.2 = $960,000
Right now, the equity is only worth: V_U = $960,000/(1+40%) = $685,714.29
Therefore,

r_E = (new-old)/old = new/old - 1 = ($960,000/$685,714.29)-1=40%

The return to the levered equity is higher because leverage always increases return and increases risk.

We can understand this better by comparing it to Bruce’s example:

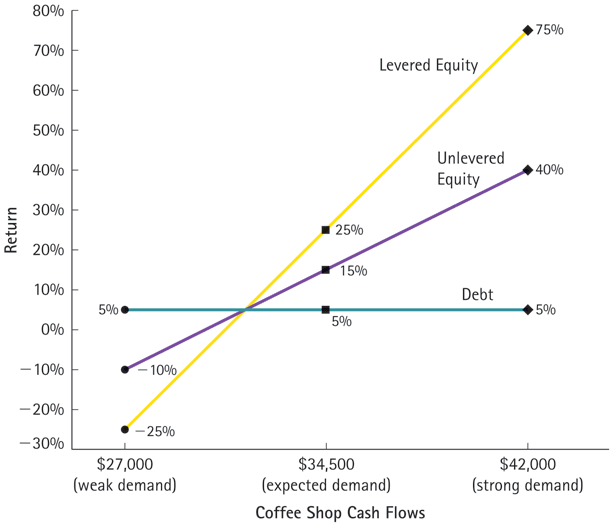
E(FCF) = 50%*27,000 + 50% * 42,000=34,500